Free Sample AMC 12

Sample AMC 12

This test is a non-timed test with 10 sample questions for you to try. Students can check the answer for each question.

If you would like to practice more, you can Sign up to get access to this course for just $39.99/month.

When you sign up, you get access to the following 3 different types of tests across all Courses:

Warm up tests - these are short 5 question quizzes to help students get bite sized practices.
Full length non-times tests - these are full length quizzes with the same number of questions as in the real test.
Challenge tests - these mimic the real test with the same number of questions and timed just liked the real test.

Each test offers:

Unlimited retakes let you practice a new set of questions with each attempt.
Detailed results of each attempt to help track progress.

If you still need help, you can always Enroll for our classes and get live help with any topic from the test.

Click the Start button to begin this sample test.

1 / 10

1) For what value of x does ${10^x} \cdot {100^{2x}} = {1000^5}$ ?

A) 1

B) 2

C) 3

D) 4

E) 5

2 / 10

2) The remainder can be defined for all real numbers x and y with $y \ne 0$ by ${\text{rem}}\left( {x,y} \right) = x - y\left\lfloor {\frac{x}{y}} \right\rfloor$ where $\left\lfloor {\frac{x}{y}} \right\rfloor$ denotes the greatest integer less than or equal to $\frac xy$ . What is the value of $\text {rem}( \frac 38, -\frac25)$ ?

A) $-\frac38$

B) $-\frac1{40}$

C) 0

D) $\frac38$

E) $\frac{31}{40}$

3 / 10

3) What is the value $\frac{2a^{-1}+\frac{a^{-1}}{2}}{a}$ when $a= \frac{1}{2}$ ?

A) 1

B) 2

C) $\frac52$

D) 10

E) 20

4 / 10

4) Pablo buys popsicles for his friends. The store sells single popsicles for $1 each, 3-popsicle boxes for $2, and 5-popsicle boxes for $3. What is the greatest number of popsicles that Pablo can buy with $8?

A) 8

B) 11

C) 12

D) 13

E) 15

Let $s$ be the number of single popsicles purchased, $t$ be the number of 3-popsicle boxes purchased, and $f$ be the number of 5-popsicle boxes purchased.
The cost of the popsicles is given by the equation:
$C = 1 \cdot s + 2 \cdot t + 3 \cdot f$
Pablo has $8, so the total cost must be less than or equal to 8:
$s + 2t + 3f \le 8$

The total number of popsicles Pablo buys is:
$N = 1 \cdot s + 3 \cdot t + 5 \cdot f$
We want to maximize $N$ subject to the cost constraint $s + 2t + 3f \le 8$ , where $s, t, f$ are non-negative integers.

To maximize the number of popsicles for a fixed amount of money, we should prioritize the options that give the most popsicles per dollar. Let's calculate the cost per popsicle for each option:
- Single popsicle: $1 / 1 = 1$ dollar per popsicle.
- 3-popsicle box: $2 / 3 \approx 0.67$ dollars per popsicle.
- 5-popsicle box: $3 / 5 = 0.6$ dollars per popsicle.

The 5-popsicle boxes are the most cost-effective, followed by the 3-popsicle boxes, and then the single popsicles. So, we should try to buy as many 5-popsicle boxes as possible first.

Let's explore the possible number of 5-popsicle boxes ( $f$ ) Pablo can buy:

Case 1: Pablo buys $f=2$ boxes of 5-popsicles.
The cost is $3f = 3(2) = 6$ .
The remaining money is $8 - 6 = 2$ .
With the remaining $2, Pablo wants to buy more popsicles. He should prioritize the 3-popsicle boxes next.
A 3-popsicle box costs $2$ . He has exactly $2 left.
He can buy $t=1$ box of 3-popsicles. The cost is $2(1) = 2$ .
The remaining money is $2 - 2 = 0$ . He cannot buy any single popsicles ( $s=0$ ).
Total cost = $3(2) + 2(1) + 1(0) = 6 + 2 + 0 = 8$ .
Total number of popsicles = $5f + 3t + s = 5(2) + 3(1) + 0 = 10 + 3 + 0 = 13$ .

If Pablo didn't buy the 3-popsicle box with the remaining $2, he could buy single popsicles.
He has $2 left, so he can buy $s=2$ single popsicles. Cost is $1(2)=2$ .
Total cost = $3(2) + 2(0) + 1(2) = 6 + 0 + 2 = 8$ .
Total number of popsicles = $5(2) + 3(0) + 2 = 10 + 0 + 2 = 12$ .
Comparing the options within Case 1, buying one 3-popsicle box yields more popsicles (13 vs 12).

Case 2: Pablo buys $f=1$ box of 5-popsicles.
The cost is $3f = 3(1) = 3$ .
The remaining money is $8 - 3 = 5$ .
With the remaining $5, Pablo should buy 3-popsicle boxes first.
Each 3-popsicle box costs $2$ . He can buy $t = \lfloor 5/2 \rfloor = 2$ boxes.
The cost of 2 boxes is $2t = 2(2) = 4$ .
The remaining money is $5 - 4 = 1$ .
With $1, he can buy $s=1$ single popsicle.
Total cost = $3(1) + 2(2) + 1(1) = 3 + 4 + 1 = 8$ .
Total number of popsicles = $5f + 3t + s = 5(1) + 3(2) + 1 = 5 + 6 + 1 = 12$ .

Case 3: Pablo buys $f=0$ boxes of 5-popsicles.
The cost is $3f = 3(0) = 0$ .
The remaining money is $8 - 0 = 8$ .
With $8, Pablo should buy 3-popsicle boxes first.
Each 3-popsicle box costs $2$ . He can buy $t = \lfloor 8/2 \rfloor = 4$ boxes.
The cost of 4 boxes is $2t = 2(4) = 8$ .
The remaining money is $8 - 8 = 0$ . He cannot buy any single popsicles ( $s=0$ ).
Total cost = $3(0) + 2(4) + 1(0) = 0 + 8 + 0 = 8$ .
Total number of popsicles = $5f + 3t + s = 5(0) + 3(4) + 0 = 0 + 12 + 0 = 12$ .

Comparing the maximum number of popsicles from each case:
Case 1 ( $f=2$ ): Maximum 13 popsicles.
Case 2 ( $f=1$ ): Maximum 12 popsicles.
Case 3 ( $f=0$ ): Maximum 12 popsicles.

The greatest number of popsicles Pablo can buy is 13. This occurs when he buys two 5-popsicle boxes and one 3-popsicle box ( $f=2, t=1, s=0$ ). The total cost is $3(2) + 2(1) = 6+2 = 8$ . The total number of popsicles is $5(2) + 3(1) = 10+3 = 13$ .

Final Answer: The final answer is $\boxed{13}$

5 / 10

5) The sum of two nonzero real numbers is 4 times their product. What is the sum of the reciprocals of the two numbers?

A) 1

B) 2

C) 4

D) 8

E) 12

6 / 10

6) Ms. Carroll promised that anyone who got all the multiple choice questions right on the upcoming exam would receive an A on the exam. Which of these statements necessarily follows logically?

A) If Lewis did not receive an A, then he got all of the multiple choice questions wrong.

B) If Lewis did not receive an A, then he got at least one of the multiple choice questions wrong.

C) If Lewis got at least one of the multiple choice questions wrong, then he did not receive an A.

D) If Lewis received an A, then he got all of the multiple choice questions right.

E) If Lewis received an A, then he got at least one of the multiple choice questions right.

Let P be the statement "A student got all the multiple choice questions right on the exam".
Let Q be the statement "A student received an A on the exam".

Ms. Carroll's promise can be written as a logical implication:
P $\implies$ Q
This means "If a student got all the multiple choice questions right, then the student received an A".

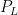We are looking for a statement that necessarily follows logically from P $\implies$ Q. This means we are looking for a statement that must be true whenever P $\implies$ Q is true. Let's apply this to the student Lewis. Let $P_L$ be "Lewis got all the multiple choice questions right" and $Q_L$ be "Lewis received an A". The given statement for Lewis is $P_L \implies Q_L$ .

Now let's examine each option:

A: "If Lewis did not receive an A, then he got all of the multiple choice questions wrong."
This statement is of the form $\neg Q_L \implies R_L$ , where $R_L$ is the statement "Lewis got all of the multiple choice questions wrong".
The negation of 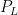$P_L$ (Lewis got all MC questions right) is $\neg P_L$ (Lewis got at least one MC question wrong).
The contrapositive of $P_L \implies Q_L$ is $\neg Q_L \implies \neg P_L$ . This means if Lewis did not receive an A, then he got at least one MC question wrong.
Getting all questions wrong ( $R_L$ ) implies getting at least one question wrong ( $\neg P_L$ ), but getting at least one question wrong ( $\neg P_L$ ) does not imply getting all questions wrong ( $R_L$ ).
So, $\neg Q_L \implies \neg P_L$ is true, but $\neg Q_L \implies R_L$ is not necessarily true. Lewis could have missed just one question and not received an A.

B: "If Lewis did not receive an A, then he got at least one of the multiple choice questions wrong."
This statement is of the form $\neg Q_L \implies \neg P_L$ .
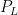As mentioned above, $\neg P_L$ is the negation of $P_L$ ("Lewis got all the multiple choice questions right"). The negation is indeed "Lewis got at least one of the multiple choice questions wrong."
The statement $\neg Q_L \implies \neg P_L$ is the contrapositive of the original statement $P_L \implies Q_L$ . The contrapositive is logically equivalent to the original implication.
Therefore, statement B necessarily follows logically.

C: "If Lewis got at least one of the multiple choice questions wrong, then he did not receive an A."
This statement is of the form $\neg P_L \implies \neg Q_L$ .
This is the inverse of the original statement $P_L \implies Q_L$ . The inverse is not logically equivalent to the original statement.
Ms. Carroll's promise only states what happens if Lewis gets all questions right. It does not state what happens if he gets any wrong. He might still get an A based on other criteria or parts of the exam.
Therefore, statement C does not necessarily follow logically.

D: "If Lewis received an A, then he got all of the multiple choice questions right."
This statement is of the form $Q_L \implies P_L$ .
This is the converse of the original statement $P_L \implies Q_L$ . The converse is not logically equivalent to the original statement.
Ms. Carroll's promise guarantees an A if all MC questions are right, but it doesn't exclude other ways of getting an A. Lewis might have received an A even if he missed some MC questions.
Therefore, statement D does not necessarily follow logically.

E: "If Lewis received an A, then he got at least one of the multiple choice questions right."
This statement is of the form $Q_L \implies \neg R_L$ , where $R_L$ is "Lewis got all of the multiple choice questions wrong". So $\neg R_L$ is "Lewis got at least one MC question right".
Does $P_L \implies Q_L$ logically imply $Q_L \implies \neg R_L$ ?
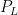Consider a scenario where Lewis got all MC questions wrong ( $R_L$ is true). In this case, $P_L$ ("Lewis got all MC questions right") is false. The implication $P_L \implies Q_L$ is therefore true (since False $\implies$ Anything is true). Now, suppose Lewis still received an A ( $Q_L$ is true), perhaps due to exceptional performance on other parts of the exam. In this scenario, $P_L \implies Q_L$ is true, $Q_L$ is true, and $R_L$ is true. Statement E says $Q_L \implies \neg R_L$ . But we have $Q_L$ true and $\neg R_L$ false (since $R_L$ is true). So $Q_L \implies \neg R_L$ is false in this scenario.
Therefore, statement E does not necessarily follow logically.

The only statement that is logically equivalent to the original statement is the contrapositive. Statement B is the contrapositive.

Final Answer: The final answer is $\boxed{B}$

7 / 10

7) Jerry and Silvia wanted to go from the southwest corner of a square field to the northeast corner. Jerry walked due east and then due north to reach the goal, but Silvia headed northeast and reached the goal walking in a straight line. Which of the following is closest to how much shorter Silvia’s trip was, compared to Jerry’s trip?

A) 30%

B) 40%

C) 50%

D) 60%

E) 70%

8 / 10

8) At a gathering of 30 people, there are 20 people who all know each other and 10 people who know no one. People who know each other hug, and people who do not know each other shake hands. How many handshakes occur?

A) 240

B) 245

C) 290

D) 480

E) 490

Let $N=30$ be the total number of people at the gathering. The people are divided into two groups:
Let $A$ be the set of 20 people who all know each other. So, $|A| = 20$ .
Let $B$ be the set of 10 people who know no one. So, $|B| = 10$ .
The total number of people is $|A| + |B| = 20 + 10 = 30$ .

The rules for interaction between any pair of people are:
1. If two people know each other, they hug.
2. If two people do not know each other, they shake hands.

We assume the relationship "knowing each other" is symmetric. If person X knows person Y, then person Y knows person X. The statement "People who know each other hug, and people who do not know each other shake hands" implies this symmetry, as it assigns a single interaction type to each pair.

We want to find the total number of handshakes that occur. A handshake occurs between two people if and only if they do not know each other. Let's analyze the interactions between pairs of people based on their group membership:

1. Interaction between two people from Group A:
Let $a_1, a_2 \in A$ be two different people from Group A. The problem states that everyone in Group A knows each other. Thus, $a_1$ and $a_2$ know each other. According to the rules, they hug.
Number of pairs within Group A is $\binom{20}{2} = \frac{20 \times 19}{2} = 190$ . There are 190 hugs within Group A.
Number of handshakes within Group A = 0.

2. Interaction between two people from Group B:
Let $b_1, b_2 \in B$ be two different people from Group B. The problem states that people in Group B know no one. This means $b_1$ does not know $b_2$ , and $b_2$ does not know $b_1$ . Since they do not know each other, they shake hands.
Number of pairs within Group B is $\binom{10}{2} = \frac{10 \times 9}{2} = 45$ .
Number of handshakes within Group B = 45.

3. Interaction between one person from Group A and one person from Group B:
Let $a \in A$ and $b \in B$ . Since person $b$ knows no one, $b$ does not know $a$ . Due to the symmetry of the relationship, $a$ also does not know $b$ . Since they do not know each other, they shake hands.
The number of such pairs is $|A| \times |B| = 20 \times 10 = 200$ .
Number of handshakes between Group A and Group B = 200.

To find the total number of handshakes, we sum the number of handshakes from all possible types of pairs:
Total Handshakes = (Handshakes within A) + (Handshakes within B) + (Handshakes between A and B)
Total Handshakes = $0 + 45 + 200 = 245$ .

The total number of interactions (hugs + handshakes) is $\binom{30}{2} = \frac{30 \times 29}{2} = 435$ .
Total Hugs = Hugs within A = 190.
Total Handshakes = 245.
Total Interactions = $190 + 245 = 435$ . This confirms our calculation.

The total number of handshakes that occur is 245.

Final Answer: The final answer is $\boxed{245}$

9 / 10

9) Joy has 30 thin rods, one each of every integer length from 1 cm through 30 cm. She places the rods with lengths 3 cm, 7 cm, and 15 cm on a table. She then wants to choose a fourth rod that she can put with these three to form a quadrilateral with positive area. How many of the remaining rods can she choose as the fourth rod?

A) 16

B) 17

C) 18

D) 19

E) 20

10 / 10

10) Define a function on the positive integers recursively by f(1) = 2, f(n) = f(n − 1) + 1 if n is even, and f(n) = f(n − 2) + 2 if n is odd and greater than 1. What is f(2017).

A) 2017

B) 2018

C) 4034

D) 4035

E) 4036

We are compiling your score. You will soon see your results...

Your score is

0%

Exit

Free Sample AMC 12

Report a question